¡Hola a todos! Seguro que os acordáis de la famosa entrada que hice hace poco sobre cómo convertir unidades de medida de longitud, masa y volumen. Pues bien, hoy lo vamos a aplicar a otras unidades de medida que también se usan en la vida diaria, como son las de superficie y las de volumen. Pero al hablar de volumen, hablamos del contenido tridimensional de un objeto. ¡Vamos allá!
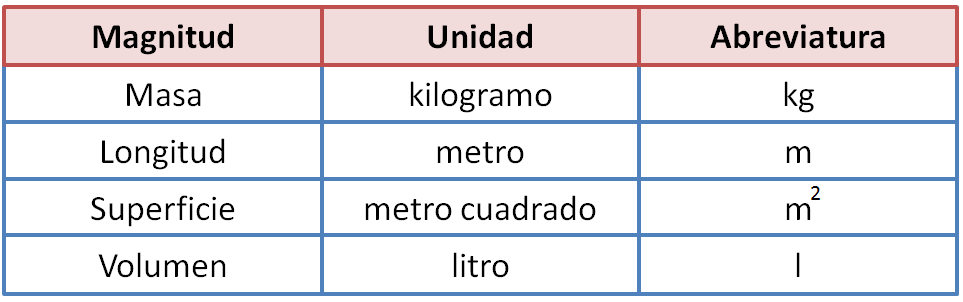
Seguro que os acordáis de las unidades que vimos hace bien poco, que eran longitud, masa y capacidad, según esta tabla, aunque la capacidad se puede ver como volumen de un líquido. De todos modos, en esta entrada os voy a enseñar cómo manejar la tabla en un caso de éstos para que lo tengáis en cuenta.
Como veis, la tabla es parecida a la de la otra vez, pero tiene cambios sustanciales en la forma de representar los números, las unidades y las cantidades a transformar, ya que las unidades son cuadráticas. Os indico cómo funciona:
Ejemplo 1: Se nos pide que pasemos la cantidad indicada de decámetros cuadrados a kilómetros cuadrados. El método es el mismo que el de la otra vez, pero con una variación sustancial. Al ser una unidad cuadrática, en cada casilla tenemos que incluir 2 CIFRAS. Por esto, podemos ver que debajo de cada casilla tenemos 2 huecos. Después de ello, el procedimiento para translocar cantidades es el mismo. Situamos la cifra de las unidades en el primer hueco empezando por la derecha, y desde ahí, todas las demás cifras detrás. En el caso de que nos falten huecos sin rellenar, ponemos 0s. A la hora de colocar la coma, la pondremos en el primer hueco empezando por la derecha, entre unidad y unidad, como vemos con la doble raya roja del ejemplo 1 de la tabla. Por tanto, la conversión sería 0'1922 kilómetros cuadrados, puesto que cada cambio de unidad supone 2 saltos en la tabla.
Ejemplo 2: Esta demostración de que, cuando pasamos de unidades lineales a unidades cuadráticas, es beneficioso a veces poner el número del resultado en notación científica. Habiendo realizado el mismo proceso del ejemplo 1, vemos que la cantidad es 21560000 milímetros cuadrados, un número muy muy grande. Para colocarlo en notación científica, colocamos la primera cifra del resultado, en este caso el 2, sacamos 3 decimales, y multiplicamos por la unidad seguida de ceros. En el exponente debemos poner la cantidad de cifras que se hayan quedado detrás de la coma. Como en este caso son 7, es x10 elevado a 7. Y por supuesto, al final, milímetros cuadrados. Cualquiera de las dos maneras sería la correcta a la hora de resolver el ejercicio.
Para las unidades de volumen os dejo este vídeo que lo explica muy bien, pero si queremos hacerlo con la tabla, tenemos que incluir 3 huecos por cada unidad que vayamos a saltar, ya que estamos hablando de que la medida es cúbica. Por esto, teniendo en cuenta la tabla de arriba, podríamos convertir exactamente igual, solo que teniendo en cuenta que ahora son 3 cifras por unidad en vez de una.
¡Espero que os haya servido y nos vemos en otra más!