¡Bienvenidos una vez más! Hoy vamos a ver uno de mis temas favoritos, ya que como es íntegramente de números y Matemáticas... Vamos a ver qué importancia tienen los números en Educación Primaria.
El concepto de número es uno de los más abstractos que existen. Se dicen que subyacen a todo el proceso de medición, ordenación, operación... Y el cálculo numérico, por tanto, es aquel que se sirve de las operaciones y procedimientos con los números para ejecutar acciones Matemáticas.
Pero si lo pensamos bien... el concepto de número engloba a cantidades tan importantes, como el 0, el 1, el número π, el número e... Y hay muchísimos más. Existen números naturales, enteros, complejos, reales, amigos, primos, gemelos... Pasamos a detallarlos con algunas de sus propiedades.
ℕ: Es el conjunto de los números naturales. Son aquellos que, fundamentalmente, sirven para contar. Se dividen en dos: N y N_0. La diferencia entre ellos es que N_0 incluye al número 0 dentro de los naturales, mientras que N lo excluye. El conjunto de los números naturales es infinito.
Como bien sabemos, hay 6 operaciones básicas para realizar con los números naturales: La suma, la resta, la multiplicación, la división, la potencia y la raíz cuadrada. De ellas, la suma y la multiplicación son las más elementales.
A continuación os dejaré unas infografías que, por orden, explicarán las propiedades de la suma y la multiplicación:
Pero para las propiedades de las potencias hay algo más que esto, ya que funcionan de manera algo diferente a la multiplicación:
Por orden, de izquierda a derecha, os las explico:
1) Todo potencia de base 1 elevada a N siempre es 1.
2) Todo número elevado a 1 es sí mismo.
3) Todo número A elevado a 0, con A distinto de 0, es 1. (Esto no es cierto si tenemos en cuenta que el límite de A cuando A tiende a 0 es 1 por la propia regla. Ahora, 0 elevado a 0 es otro cantar si hablamos de indeterminación en vez de resultado 1)
4) En una multiplicación de potencias de la misma base, se deja la base y se suman los exponentes.
5) En una división de potencias de la misma base, se deja la base y se restan los exponentes.
6) Cuando una potencia se eleva a otra potencia, se deja la base y se multiplican los exponentes.
7) Cuando una fracción se eleva a una potencia, se deja la base y se elevan tanto el numerador como el denominador al exponente.
8) Cuando un número A se eleva a -1, su resultado es su inverso en forma de fracción, con A distinto de 0 (aunque se puede entender que si A tiende a 0, el resultado es + ∞)
9) Cuando una fracción se eleva a -1, su resultado es la fracción inversa de la primera.
10) Cuando un número A se eleva a un exponente negativo distinto de 1, su resultado es la fracción inversa con denominador en forma de la potencia elevada a exponente positivo, siendo A distinto de cero. (En este caso, volveríamos al ejemplo del caso 8).
11) Cuando una fracción se eleva a un exponente negativo, su resultado es la inversa con cada factor elevado al exponente.
La resta, la división y la raíz cuadrada no comparten ninguna de estas propiedades, al tener posibles soluciones algebraicas que no sería posible encuadrar en N.
Z: Es el conjunto de los números enteros. En él se incluyen todos los números naturales (o enteros positivos), el 0 y los naturales negativos (o enteros negativos). Es un conjunto infinito y, de hecho, es un conjunto infinito más grande que el de los números naturales N.
Comparten operaciones con los números naturales y sus propiedades, pero por lo general se utiliza el valor absoluto de los números y se calcula con ellos. El valor absoluto es considerado como el número natural que no tiene signo, y que se representa con dos barras verticales en medio: 
En la potenciación surge una nueva propiedad, que dice que cualquier entero elevado a un exponente N, debe representarse así:
1) Si un entero positivo o negativo se eleva a un exponente positivo o negativo par, su potencia será positiva.
2) Si un entero positivo o negativo se eleva a un exponente negativo impar, su potencia será negativa.
En este punto entran dos conceptos básicos: Los múltiplos y los divisores y sus acompañantes, el mínimo común múltiplo y el máximo común divisor. Para hallarlos, debemos:− Dados dos números enteros a y b, se llama MCD de a y b al mayor entero que divide a ambos. Para calcularlo: se tomará el producto de los factores primos comunes con el menor exponente de sus descomposiciones.
− Dados dos números enteros a y b, se llama mcm de a y b, al menor entero que es múltiplo de ambos. Para calcularlo se tomará el producto de todos los factores primos con el mayor exponente de sus descomposiciones.
Aquí entran en juego los llamados números primos, que son todos aquellos que se pueden dividir únicamente entre 1 y entre sí mismos de forma exacta. Unidos a ellos existen los llamados criterios de divisibilidad, y junto a estos, unos números primos llamados de Mersenne, de la forma  , para N primo. Como éstos se conocen aproximadamente unos 50. El más alto sería el (M82.589.933).
, para N primo. Como éstos se conocen aproximadamente unos 50. El más alto sería el (M82.589.933).
 : Es el conjunto de los llamados números racionales, que son todos aquellos que se pueden expresar en forma de cociente de dos números enteros. En este conjunto se incluyen todos aquellos números conocidos como fracciones, que es la expresión de un cociente de dos números.
: Es el conjunto de los llamados números racionales, que son todos aquellos que se pueden expresar en forma de cociente de dos números enteros. En este conjunto se incluyen todos aquellos números conocidos como fracciones, que es la expresión de un cociente de dos números.
Las fracciones también tienen sus propiedades, que serían:
1) La multiplicación de fracciones se realiza multiplicando numeradores y denominadores simultáneamente.
2) La división de fracciones se puede realizar operando el producto cruzado de ambas.
3) La suma (o resta) de fracciones con igual denominador se realiza dejando el mismo denominador y sumando los numeradores.
4) La suma de fracciones con distinto denominador se puede realizar obteniendo el mcm de los denominadores y multiplicando cada numerador por el factor sobrante.
5) Una fracción irreducible es aquella que no se puede dividir más veces por el mismo factor primo. De hecho, la fracción simplificable es aquella que se puede dividir por uno o más factores primos comunes al numerador y al denominador.
6) Cuando dos fracciones son equivalentes, su producto cruzado también lo es.
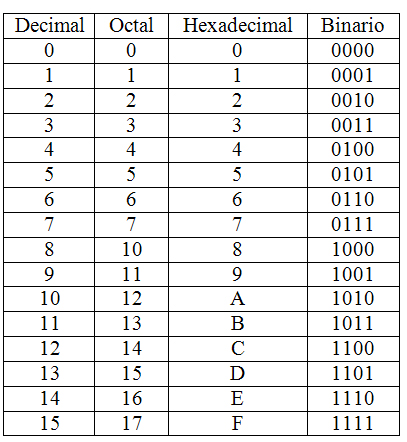
Al hablar de números racionales también encontramos los números decimales, que serán racionales o irracionales (I) en función de su desarrollo decimal. Por esto, los números decimales exactos, como el 1'25 o el 0'97 son racionales, mientras que π, al tener infinitos decimales no periódicos, se dice que es irracional y trascendente.El sistema de numeración decimal (o de base 10) no es el único que existe. Hay infinitos más, pero los más conocidos son el binario (que se usa en informática), el octal (base 8) y el hexadecimal (base 16), que se usan también en informática, pero específicamente en criptografía, y el sistema en base 36 o alfanumérico, que es la base de múltiples operaciones y procesos matemáticos superiores.
En Educación Primaria nos interesan otros dos que pasan algo más desapercibidos, como son el sistema sexagesimal (base 60), que tiene como su origen la división del círculo en 360 partes (2πrad), o el sistema de numeración romana (I, V, X, L, C, D y M), que actualmente se utiliza para nombrar siglos de la historia, entre otros usos.
La relación entre los infinitos números queda demostrada en esta pequeña infografía. Cada conjunto es más grande que el anterior, de ahí que haya infinitos más grandes que otros. En Educación Primaria nos detendremos en R, mientras que en Educación Secundaria y Bachillerato introduciremos la idea de C, o los números complejos.
El Decreto 81/2022, aunque no contempla los números enteros como parte de los saberes básicos del currículo, englobaría todos estos conceptos matemáticos dentro del Sentido Numérico. Además, estos contenidos básicos para los alumnos y alumnas de Primaria, favorecen al desarrollo de las competencias clave del currículo, en especial la Competencia Matemática y Competencia en Ciencia, Tecnología e Ingeniería o STEAM/STEM.
¡WOW! Menudo tema nos ha quedado... ¿Qué os parece? Si os digo la verdad, he disfrutado muchísimo escribiendo esto para todos vosotros... La pena es que ya solo quedan 6 temas para acabar con esto... Que no son pocos eh... Pero ya va quedando menos. ¡Nos vemos!
















































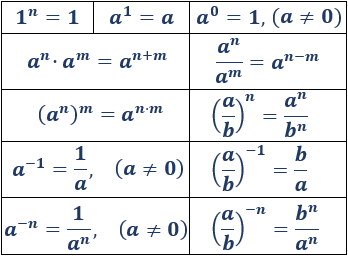


 , para N primo. Como éstos se conocen aproximadamente unos 50. El más alto sería el
, para N primo. Como éstos se conocen aproximadamente unos 50. El más alto sería el 
 : Es el conjunto de los llamados números racionales, que son todos aquellos que se pueden expresar en forma de cociente de dos números enteros. En este conjunto se incluyen todos aquellos números conocidos como fracciones, que es la expresión de un cociente de dos números.
: Es el conjunto de los llamados números racionales, que son todos aquellos que se pueden expresar en forma de cociente de dos números enteros. En este conjunto se incluyen todos aquellos números conocidos como fracciones, que es la expresión de un cociente de dos números.