Tema 24: Evolución de la percepción espacial en Educación Primaria

¡Bienvenidos de nuevo! Una vez más estamos aquí, entrando ya en la recta final del temario, puesto que ya solo quedan 5 temas por ver. Hoy nos pararemos en la evolución de la percepción espacial en Educación Primaria.

La percepción espacial va evolucionando al mismo tiempo que se desarrollan los alumnos en Educación Primaria. Las Matemáticas contribuyen fundamentalmente a este desarrollo de la percepción, especialmente la rama de geometría. En el Estadio de las Operaciones Concretas de Piaget, no es hasta los 10 años donde se puede trabajar el concepto de bidimensional y tridimensional.

En geometría tenemos multitud de conceptos que debemos estudiar para enseñar en el colegio. Pasamos a describirlos:

Primero, hay que saber que una recta es una línea que une dos puntos con una longitud mínima. Así, tenemos 4 tipos de rectas en el plano:

Paralelas: No se cortan nunca.

Secantes: Se cortan en un único punto.

Perpendiculares: Se cortan en un único punto, pero éste forma un ángulo recto.

Coincidentes: Son la misma recta, al tener todos sus puntos en común.

Un ángulo euclidiano es la inclinación mutua de dos líneas que se encuentran en un punto. Este punto  se denomina ángulo. También tenemos diferentes clasificaciones:

Recto: Mide 90º.

Agudo: Mide más de 0º y menos de 90º.

Obtuso: Mide más de 90º y menos de 180º.

Llano: Mide 180º.

Completo: Mide 360º.

Cóncavo: Mide más de 180º y menos de 360º.

También hay otras clasificaciones, como los complementarios, que son dos ángulos unidos que suman 90º, y los suplementarios, que suman 180º. Los suplementarios también suelen ser adyacentes. Los ángulos opuestos por el vértice son aquellos que tienen el vértice común y sus lados son opuestos dos a dos. Mientras, los consecutivos tienen el vértice y uno de los lados.

Ahora pasamos a ver otro concepto fundamental en geometría: el polígono. Éste es denominado como una figura plana cerrada por segmentos rectilíneos. Sus elementos principales son los lados, los vértices, los ángulos interiores, y las diagonales. Para calcular el número de diagonales de un polígono regular de N lados, debemos realizar la siguiente operación: D = [N . (N-3)]/2

En un polígono podemos encontrar dos medidas fundamentales: el perímetro, que es la suma de todos los lados, y el área, que es la superficie que cubre el polígono en su interior. En un polígono regular de 5 o más lados, el cálculo del área se realiza multiplicando el perímetro por su apotema y dividiéndolo por 2.

 

Esta infografía que os he dejado aquí abajo explica muy bien el siguiente elemento geométrico que vamos a tratar: el triángulo. Tiene diferentes clasificaciones que vemos aquí abajo:

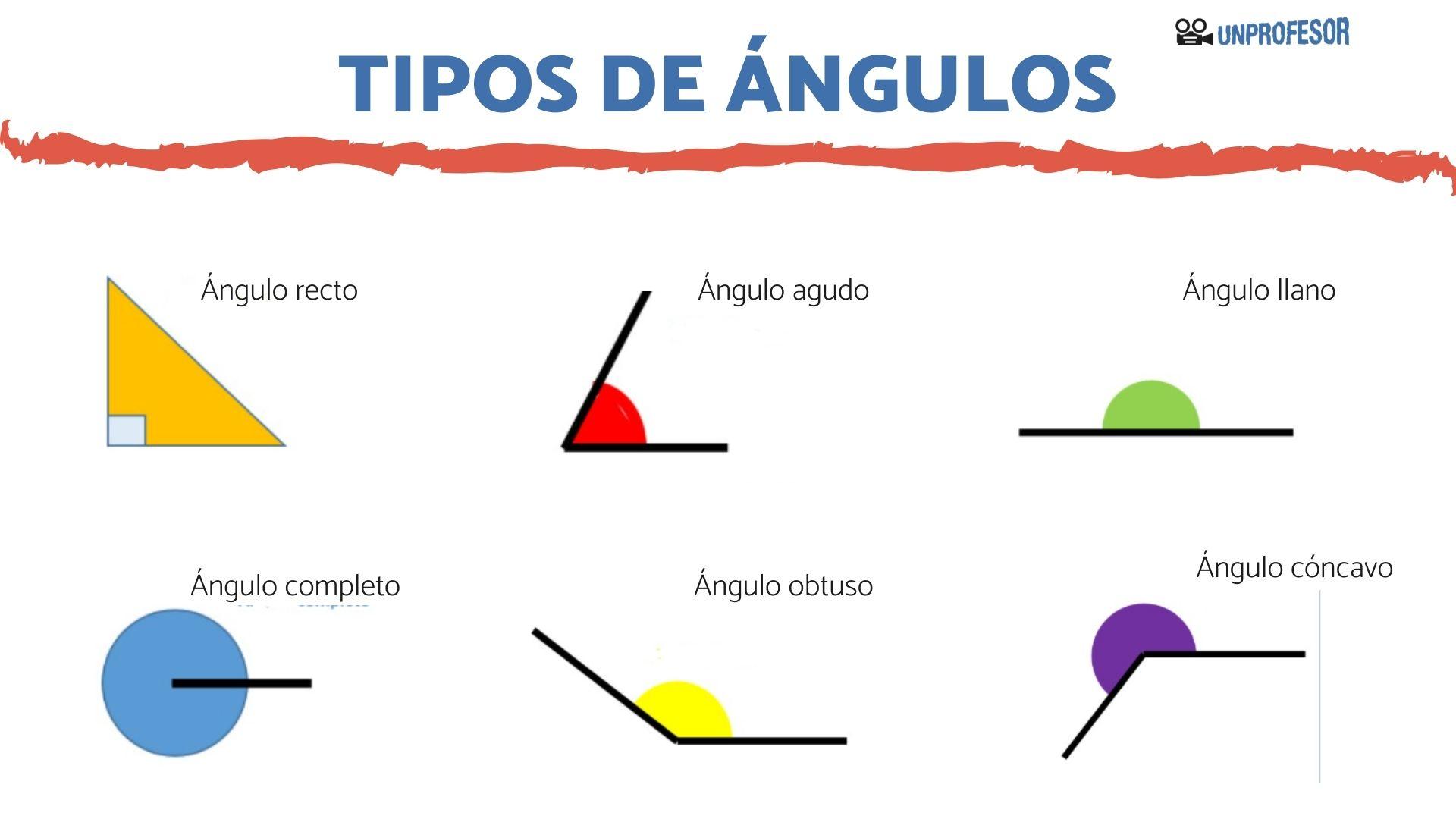
Aquí coge una importancia vital el conocidísimo Teorema de Pitágoras, que enuncia que la suma de los catetos al cuadrado es igual al cuadrado de la hipotenusa. Este teorema exclusivamente se puede aplicar en los triángulos rectángulos. Además, debemos saber que la suma de los ángulos interiores de un triángulo es de 180º.

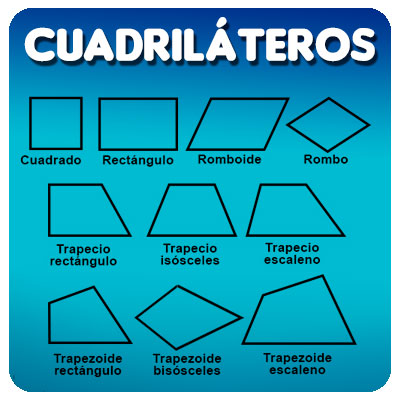
Los cuadriláteros son polígonos de 4 lados. Sus lados suman un total de 360º, y tienen diferentes clasificaciones en función de sus lados y ángulos. Así, tenemos:

− Cuadrado: Tiene todos los lados y los ángulos iguales. Es el polígono regular de cuatro lados.

− Rectángulo: Tiene los lados iguales dos a dos y todos los ángulos iguales.

− Rombo: Tiene todos los lados iguales y los ángulos iguales dos a dos. Tiene dos diagonales y siempre una es mayor que la otra. En este caso se las denomina Diagonal mayor (D) y diagonal menor (d).

− Romboide: Tiene los lados iguales dos a dos y los ángulos iguales dos a dos.

− Trapecios: Tienen dos lados paralelos y otros dos no paralelos. A los lados paralelos se los denomina bases y puesto que uno debe ser mayor que el otro se los denomina Base mayor (B) y base menor (b). La altura (h) es la distancia entre la Base mayor y la menor. Los trapecios pueden ser:

o Trapecio isósceles: Los lados no paralelos miden lo mismo.
o Trapecio rectángulo: Uno de cuatro ángulos es recto.
o Trapecio escaleno: No hay ángulos rectos ni lados iguales.
• Trapezoides: No tienen lados paralelos.

Cada uno de ellos tiene su propia fórmula de cálculo de áreas, que imagino que todos conoceréis.

Otro de los elementos fundamentales de la geometría es el círculo y la circunferencia. Ésta es una línea curva plana y cerrada, cuyos puntos equidistan del centro en todo su perímetro. Sus elementos fundamentales son el radio, el diámetro (el doble del radio), la cuerda y el arco.

Dentro del círculo también hay determinados elementos, que conciben diferentes aspectos de éste. El círculo es definido como la superficie que ocupa una circunferencia.

Los elementos del círculo los podréis encontrar descritos en este vídeo, que los explica correctamente. Para calcular el perímetro y el área de la circunferencia y el círculo respectivamente debemos echar mano del número π, de tal manera que el perímetro se calcula haciendo 2πr, que equivale a 360º, y el área con la fórmula πr^2.

 Dados un punto P y una circunferencia C, el punto P puede ser:

- Interior a la circunferencia si su distancia al centro O es menor que el radio de la circunferencia si su distancia al centro O es igual que el radio.

- Exterior a la circunferencia si su distancia al centro O es mayor que el radio.

Dados una recta r y una circunferencia C, la recta r puede ser:

• Secante si corta a la circunferencia en dos puntos.

• Tangente si corta a la circunferencia en un solo punto.

• Exterior si no corta a la circunferencia.

Dadas dos circunferencias y según las posiciones relativas que pueden tomar, son:

• Secantes: Si tienen dos puntos en común.

• Tangentes interiores, si tienen un punto en común y todos los puntos de una
de las circunferencias son interiores a la otra.

• Tangentes exteriores, si tienen un punto en común y todos los puntos de
ambas circunferencias son exteriores respecto a la otra.

• Exteriores si no tienen puntos en común. 

• Concéntricas, si tienen el mismo centro en común.

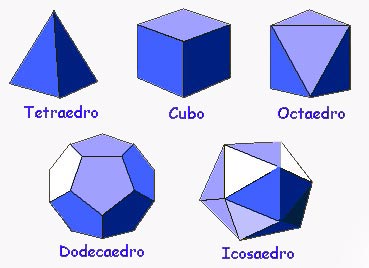
Ahora pasamos a la tridimensionalidad a través de los poliedros regulares, que son cuerpos geométricos cerrados limitados por caras planas, todas ellas polígonos regulares. Los principales son estos 5 de aquí:

Tetraedro: 4 caras, todas ellas triángulos equiláteros.

Cubo: 6 caras, todas ellas cuadrados.

Octaedro: 8 caras, todas ellas triángulos equiláteros.

Dodecaedro: 12 caras, todas ellas pentágonos regulares.

Icosaedro: 20 caras, todas ellas triángulos equiláteros.

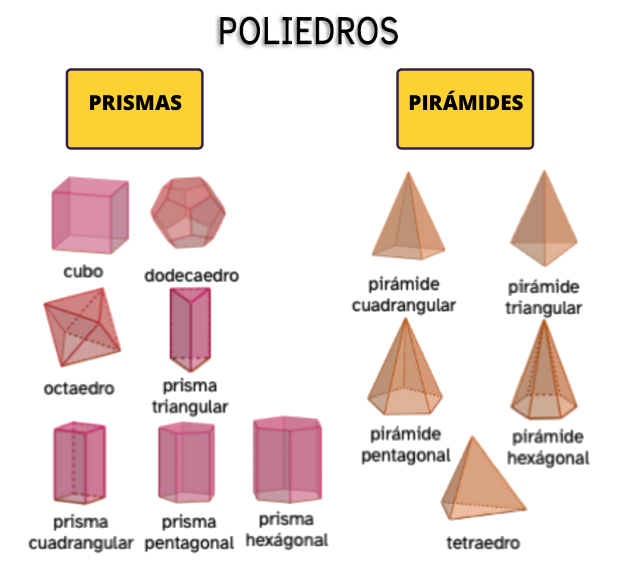
Otros poliedros son: 

 

• El prisma. Es un poliedro que tiene dos caras iguales y paralelas llamadas bases. El resto de caras son paralelogramos que se denominan caras laterales. La altura de un prisma es la distancia que hay entre sus bases. Se dice que un prisma es recto cuando las caras laterales son perpendiculares a las bases. En
caso contrario será oblicuo. Su área total se calcula sumando el doble del área de una de sus bases (AB) más el área de todas sus caras laterales (AL). AT = 2 AB + AL. El volumen viene determinado por el producto del área de una de sus bases (AB) por la altura (h) del prisma: V = AB . h 

• La pirámide. Es un poliedro que tiene una única base que es un polígono cualquiera y por caras laterales triángulos con un vértice común que se denomina vértice de la pirámide. Una pirámide es regular cuando la base es un polígono regular y el vértice está sobre el centro del polígono base. Su área total se calcula sumando el área de su base (AB) más el área de todas sus caras laterales (AL): AT = AB + AL. Su volumen viene determinado por la tercera parte del producto del área de su base (AB) por la altura (h) de la pirámide: V = 1/3 AB . h.

Los cuerpos de revolución son otros cuerpos geométricos, que se generan al girar una figura plana alrededor de un eje. Los principales son el cilindro, el cono y la esfera.

- El cilindro se genera a partir del giro de un paralelogramo alrededor de uno de sus lados, generalmente un rectángulo o un romboide.

- El cono se genera a partir del giro de un triángulo rectángulo a partir de uno de sus catetos.

- La esfera se genera a partir de un semicírculo alrededor de su diámetro.

Cada uno de ellos tiene una serie de fórmulas y algoritmos para calcular su área y su volumen. Al ser cuerpos de revolución, todos ellos dependen completamente del número π.

¿Y cómo podemos representar los cuerpos geométricos y las figuras planas? Pues a través de los llamados sistemas de representación, que definió el teórico Monge, añadiendo a las Matemáticas el término de Geometría Descriptiva.

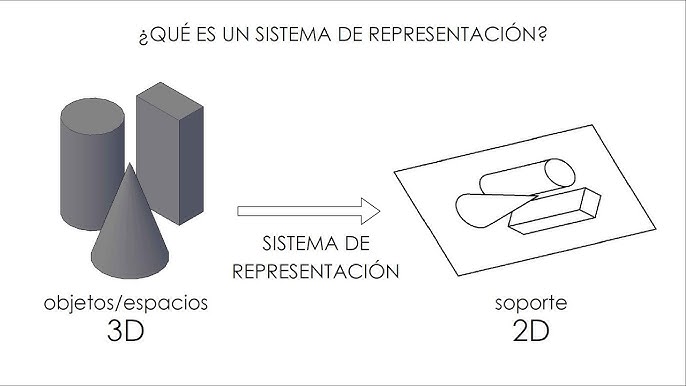
Los modelos 2D y 3D son muy variados, pero principalmente tenemos algunos que reconoceréis, como el dibujo, el croquis, la fotografía o el propio plano en sí.

Es por esto que la intervención educativa en geometría no puede ser solo conceptual, sino también basada en la realidad y representativa, y sobre todo práctica, ya que la geometría es uno de los ámbitos de las Matemáticas que más difícil resulta para el alumnado de Educación Primaria.

El Decreto 81/2022 incluye los saberes básicos relacionados con la geometría y la percepción espacial con el Bloque C: Sentido Espacial. El trabajo de la geometría contribuye al desarrollo de 5 de las 8 competencias clave del currículo: La Competencia en Comunicación Lingüística (CCL), la Competencia Matemática y Competencia en Ciencia, Tecnología e Ingeniería (STEAM/STEM), la Competencia Digital (CD), la Competencia Personal, Social y de Aprender a Aprender (CPSAA), y la Competencia Emprendedora (CE).

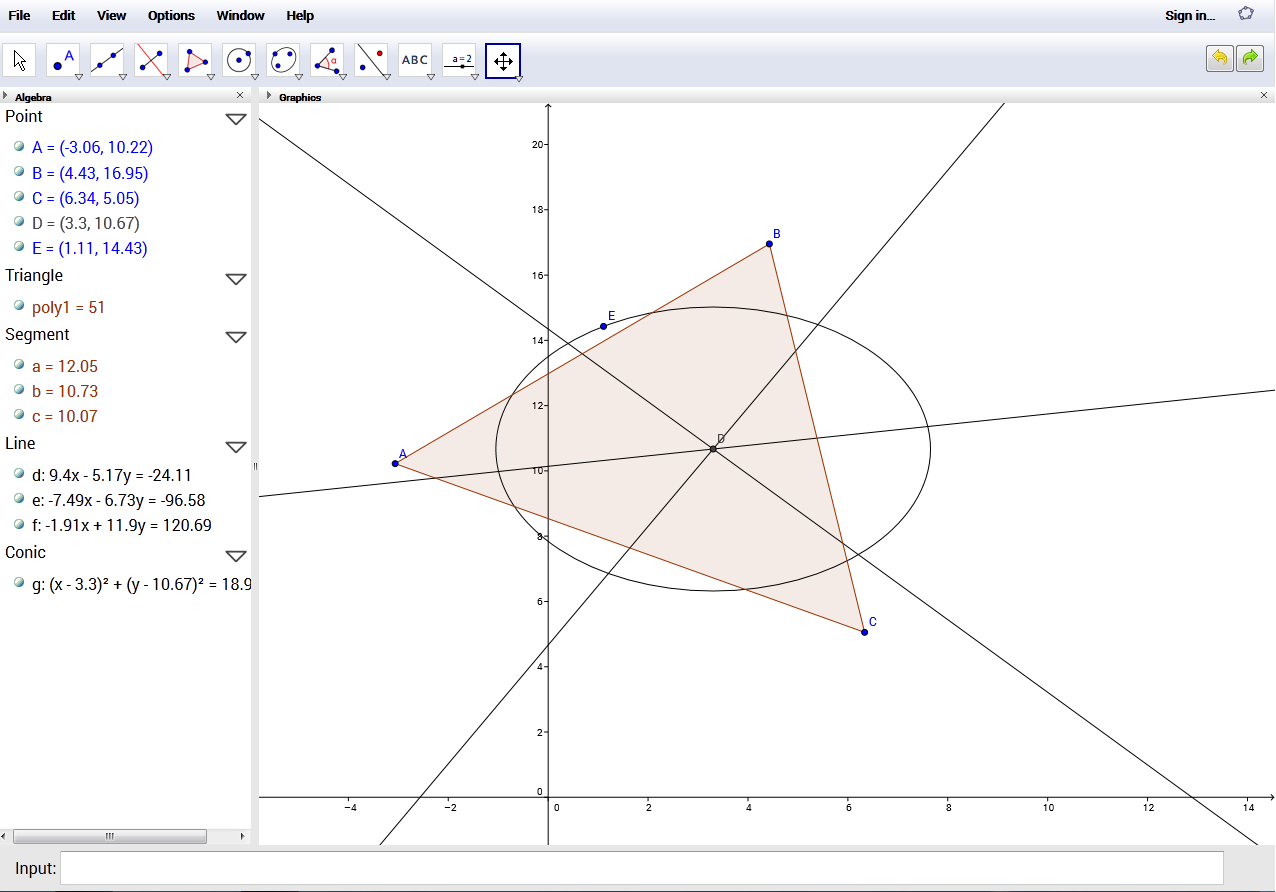
Existen múltiples recursos, tanto físicos como digitales, que permiten trabajar la geometría en el aula, como por ejemplo el Tangram o el Geoplano, pero sin duda el mejor de todos es el programa Geogebra. Tiene casi todas las funciones que se puedan necesitar en Matemáticas, desde una hoja de cálculo, un eje de coordenadas, incluso funciones en 3D para representar cuerpos geométricos. Además, como bien sabemos, los recursos TIC vienen muy bien de cara a mejorar el aprendizaje significativo de los saberes básicos del currículo.

¿Qué os parece? Este sí que ha sido un tema DENSO. Pero ya solo quedan 4... Cuenta atrás en marcha. ¡Nos vemos!