Tema 25: Recogida, organización y representación de la información en Educación Primaria

¡Bienvenidos una vez más! Por desgracia, este es el último tema de Matemáticas de nuestro camino del opositor. Hoy vamos a tratar un tema que en Educación Primaria personalmente no he visto mucho, pero que igualmente es importante, y más en la Sociedad de la Información: La Estadística.

La Estadística es la llamada ciencia de los datos. Según Spiegel, esta ciencia se encarga de estudiar los métodos científicos que permiten recoger, organizar, resumir y analizar datos, con el objetivo de sacar conclusiones válidas de ellos.

Se divide en dos subramas: La estadística descriptiva, que estudia las formas de recogida y clasificación de datos, y la estadística inferencial, que se encarga de analizar los resúmenes de datos, realizando modelos de probabilidad basados en estos datos.

La recogida de información se basa fundamentalmente en las variables, que son todos aquellos valores, tanto cualitativos como cuantitativos, que forman parte de una muestra. Ésta es el subconjunto de todos los valores existentes en una población o total de miembros de una comunidad. Esto es, que si en España viven más de 40 millones de habitantes, una muestra representativa estaría alrededor de los 20k. A partir de estas muestras, se procede a la extrapolación de los datos a la cantidad que se desee.

 

La representación de los datos de un muestreo normalmente se realiza mediante probabilidad y porcentajes. Comúnmente, los gráficos sectoriales, como este de aquí arriba, son bastante representativos a la hora de recopilar datos de interés general, como la situación económica o las intenciones de voto de una gran masa de población.

En este aspecto, la normativa educativa en Matemáticas, recoge en el Bloque E: Sentido Estocástico, los saberes básicos vinculados a la estadística y la probabilidad de sucesos. El Decreto 81/2022 no especifica demasiado en Educación Primaria, ya que ciertas variables de cálculo pueden resultar difíciles de cálculo para los alumnos de estas edades.

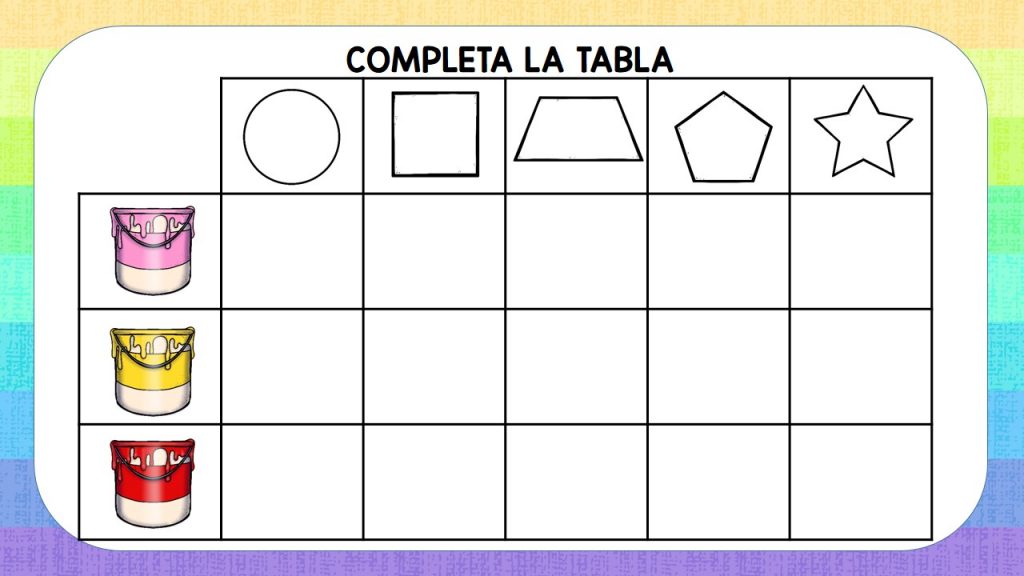
En estadística existen multitud de gráficos y tablas posibles a realizar. Para niños de 1º y 2º, las tablas de doble entrada son muy frecuentes dada su baja complejidad de interpretación y comprensión. En este ejemplo, el resultado en cada celda sería dibujar la figura de la columna pintada del color de la fila.

Para cursos superiores, se pueden hallar valores básicos dentro de las tablas de frecuencia o de doble entrada, llamados parámetros de centralización y dispersión, que muestran información sobre la situación del centro de la muestra obtenida o alrededor de toda ella, compenetrándose unos con otros. Así, los más básicos serían:

Media aritmética: Aunque la definición matemática es multiplicar por 1/N el sumatorio de todos los datos de una muestra, el concepto matemático es "el valor medio" entre todos los valores de un conjunto.

Moda: Es el valor más repetido dentro de un conjunto de valores.

Mediana: Indica cuál es el valor central de una muestra, y se calcula a partir del conjunto de valores de la misma mayores o iguales que el 50% y comparándolos con los menores o iguales que el otro 50%.

Cuartiles y percentiles: Sirven para saber qué valor de la muestra es superior al (100-x)% de los elementos de una muestra. Los más destacados son el C25 (25%), el C50 (50%) y el C75 (75%).

Desviaciones: Sirven para conocer el grado de dispersión de una muestra respecto de su distribución. La más conocida es la desviación respecto de la media, que se calcula restándole al total de subconjuntos de una muestra el valor de su media aritmética.

En el área de Estadística también se engloba a la Probabilidad. Se define como la rama ligada a la estadística mediante la Ley de Estabilidad de las Frecuencias. En experimentos de carácter aleatorio, cuantos más se hagan, más se alcanzará la frecuencia relativa de cualquier suceso de una muestra predeterminada.

Para calcular la probabilidad de que un suceso ocurra, es tan sencillo como dividir el número de resultados favorables entre el total de sucesos posibles. Así, como en el ejemplo, la probabilidad de que te toque un 7 de tréboles en la baraja de cartas francesa es 1/52.

Esta infografía que os dejo por aquí nos da una información valiosísima de las formas que tenemos de agrupar datos en gráficas. De aquí, las más conocidas, ya sean por los medios de comunicación o por su aplicación en Matemáticas, serían los gráficos de columnas, los de tarta o sectoriales, o los histogramas, que se utilizan sobre todo en aspectos relacionados con la población.

La lectura de gráficos como estos suelen ser difíciles en Educación Primaria, pero dependiendo de las variables que se utilicen para su realización, pueden disminuir esa dificultad. Para la correcta intervención educativa, se deberá ir cambiando de variables cualitativas a variantes cuantitativas de forma progresiva y, sobre todo, utilizar gráficas elementales y de fácil interpretación.

El Decreto 81/2022 y el Real Decreto 157/2022 explican que la recogida de información, así como su organización y representación, tienen múltiples aplicaciones didácticas en el currículo. Sobre todo, el hecho de interpretar datos estadísticos y de probabilidad fomenta el pensamiento científico, para poder transformar estos datos en conocimiento. Por esto, la estadística y la probabilidad tienen relación con el resto de áreas del currículo.

Las TIC son una herramienta clave en el aprendizaje de la estadística, ya que son capaces de representar adecuadamente una gran cantidad de datos y variables en gráficas muy sencillas y de fácil interpretación. De hecho, la Ley Orgánica 3/2020 (LOMLOE) indica que las TIC se encuentran dentro de los objetivos de etapa, así como su integración competencial por parte de la Competencia Digital.

Bingham en 2010 señala que el profesor se convierte en mediador entre la información que reciben sus alumnos de las TIC y sus propios alumnos. También este autor señala, entre los recursos didácticos más destacados, el uso de procesadores de textos y hojas de cálculo, y, en general, aplicaciones informáticas que pueden ser útiles para cualquier usuario de ellas.

¿Qué os ha parecido? Ya solo nos quedan 3 temas para terminar... Y además con esto cerramos la asignatura de Matemáticas. ¡Nos vemos en los temas de Valores y Artística!

Read More

Tema 24: Evolución de la percepción espacial en Educación Primaria

¡Bienvenidos de nuevo! Una vez más estamos aquí, entrando ya en la recta final del temario, puesto que ya solo quedan 5 temas por ver. Hoy nos pararemos en la evolución de la percepción espacial en Educación Primaria.

La percepción espacial va evolucionando al mismo tiempo que se desarrollan los alumnos en Educación Primaria. Las Matemáticas contribuyen fundamentalmente a este desarrollo de la percepción, especialmente la rama de geometría. En el Estadio de las Operaciones Concretas de Piaget, no es hasta los 10 años donde se puede trabajar el concepto de bidimensional y tridimensional.

En geometría tenemos multitud de conceptos que debemos estudiar para enseñar en el colegio. Pasamos a describirlos:

Primero, hay que saber que una recta es una línea que une dos puntos con una longitud mínima. Así, tenemos 4 tipos de rectas en el plano:

Paralelas: No se cortan nunca.

Secantes: Se cortan en un único punto.

Perpendiculares: Se cortan en un único punto, pero éste forma un ángulo recto.

Coincidentes: Son la misma recta, al tener todos sus puntos en común.

Un ángulo euclidiano es la inclinación mutua de dos líneas que se encuentran en un punto. Este punto  se denomina ángulo. También tenemos diferentes clasificaciones:

Recto: Mide 90º.

Agudo: Mide más de 0º y menos de 90º.

Obtuso: Mide más de 90º y menos de 180º.

Llano: Mide 180º.

Completo: Mide 360º.

Cóncavo: Mide más de 180º y menos de 360º.

También hay otras clasificaciones, como los complementarios, que son dos ángulos unidos que suman 90º, y los suplementarios, que suman 180º. Los suplementarios también suelen ser adyacentes. Los ángulos opuestos por el vértice son aquellos que tienen el vértice común y sus lados son opuestos dos a dos. Mientras, los consecutivos tienen el vértice y uno de los lados.

Ahora pasamos a ver otro concepto fundamental en geometría: el polígono. Éste es denominado como una figura plana cerrada por segmentos rectilíneos. Sus elementos principales son los lados, los vértices, los ángulos interiores, y las diagonales. Para calcular el número de diagonales de un polígono regular de N lados, debemos realizar la siguiente operación: D = [N . (N-3)]/2

En un polígono podemos encontrar dos medidas fundamentales: el perímetro, que es la suma de todos los lados, y el área, que es la superficie que cubre el polígono en su interior. En un polígono regular de 5 o más lados, el cálculo del área se realiza multiplicando el perímetro por su apotema y dividiéndolo por 2.

 

Esta infografía que os he dejado aquí abajo explica muy bien el siguiente elemento geométrico que vamos a tratar: el triángulo. Tiene diferentes clasificaciones que vemos aquí abajo:

Aquí coge una importancia vital el conocidísimo Teorema de Pitágoras, que enuncia que la suma de los catetos al cuadrado es igual al cuadrado de la hipotenusa. Este teorema exclusivamente se puede aplicar en los triángulos rectángulos. Además, debemos saber que la suma de los ángulos interiores de un triángulo es de 180º.

Los cuadriláteros son polígonos de 4 lados. Sus lados suman un total de 360º, y tienen diferentes clasificaciones en función de sus lados y ángulos. Así, tenemos:

− Cuadrado: Tiene todos los lados y los ángulos iguales. Es el polígono regular de cuatro lados.

− Rectángulo: Tiene los lados iguales dos a dos y todos los ángulos iguales.

− Rombo: Tiene todos los lados iguales y los ángulos iguales dos a dos. Tiene dos diagonales y siempre una es mayor que la otra. En este caso se las denomina Diagonal mayor (D) y diagonal menor (d).

− Romboide: Tiene los lados iguales dos a dos y los ángulos iguales dos a dos.

− Trapecios: Tienen dos lados paralelos y otros dos no paralelos. A los lados paralelos se los denomina bases y puesto que uno debe ser mayor que el otro se los denomina Base mayor (B) y base menor (b). La altura (h) es la distancia entre la Base mayor y la menor. Los trapecios pueden ser:

o Trapecio isósceles: Los lados no paralelos miden lo mismo.
o Trapecio rectángulo: Uno de cuatro ángulos es recto.
o Trapecio escaleno: No hay ángulos rectos ni lados iguales.
• Trapezoides: No tienen lados paralelos.

Cada uno de ellos tiene su propia fórmula de cálculo de áreas, que imagino que todos conoceréis.

Otro de los elementos fundamentales de la geometría es el círculo y la circunferencia. Ésta es una línea curva plana y cerrada, cuyos puntos equidistan del centro en todo su perímetro. Sus elementos fundamentales son el radio, el diámetro (el doble del radio), la cuerda y el arco.

Dentro del círculo también hay determinados elementos, que conciben diferentes aspectos de éste. El círculo es definido como la superficie que ocupa una circunferencia.

Los elementos del círculo los podréis encontrar descritos en este vídeo, que los explica correctamente. Para calcular el perímetro y el área de la circunferencia y el círculo respectivamente debemos echar mano del número π, de tal manera que el perímetro se calcula haciendo 2πr, que equivale a 360º, y el área con la fórmula πr^2.

 Dados un punto P y una circunferencia C, el punto P puede ser:

- Interior a la circunferencia si su distancia al centro O es menor que el radio de la circunferencia si su distancia al centro O es igual que el radio.

- Exterior a la circunferencia si su distancia al centro O es mayor que el radio.

Dados una recta r y una circunferencia C, la recta r puede ser:

• Secante si corta a la circunferencia en dos puntos.

• Tangente si corta a la circunferencia en un solo punto.

• Exterior si no corta a la circunferencia.

Dadas dos circunferencias y según las posiciones relativas que pueden tomar, son:

• Secantes: Si tienen dos puntos en común.

• Tangentes interiores, si tienen un punto en común y todos los puntos de una
de las circunferencias son interiores a la otra.

• Tangentes exteriores, si tienen un punto en común y todos los puntos de
ambas circunferencias son exteriores respecto a la otra.

• Exteriores si no tienen puntos en común. 

• Concéntricas, si tienen el mismo centro en común.

Ahora pasamos a la tridimensionalidad a través de los poliedros regulares, que son cuerpos geométricos cerrados limitados por caras planas, todas ellas polígonos regulares. Los principales son estos 5 de aquí:

Tetraedro: 4 caras, todas ellas triángulos equiláteros.

Cubo: 6 caras, todas ellas cuadrados.

Octaedro: 8 caras, todas ellas triángulos equiláteros.

Dodecaedro: 12 caras, todas ellas pentágonos regulares.

Icosaedro: 20 caras, todas ellas triángulos equiláteros.

Otros poliedros son: 

 

• El prisma. Es un poliedro que tiene dos caras iguales y paralelas llamadas bases. El resto de caras son paralelogramos que se denominan caras laterales. La altura de un prisma es la distancia que hay entre sus bases. Se dice que un prisma es recto cuando las caras laterales son perpendiculares a las bases. En
caso contrario será oblicuo. Su área total se calcula sumando el doble del área de una de sus bases (AB) más el área de todas sus caras laterales (AL). AT = 2 AB + AL. El volumen viene determinado por el producto del área de una de sus bases (AB) por la altura (h) del prisma: V = AB . h 

• La pirámide. Es un poliedro que tiene una única base que es un polígono cualquiera y por caras laterales triángulos con un vértice común que se denomina vértice de la pirámide. Una pirámide es regular cuando la base es un polígono regular y el vértice está sobre el centro del polígono base. Su área total se calcula sumando el área de su base (AB) más el área de todas sus caras laterales (AL): AT = AB + AL. Su volumen viene determinado por la tercera parte del producto del área de su base (AB) por la altura (h) de la pirámide: V = 1/3 AB . h.

Los cuerpos de revolución son otros cuerpos geométricos, que se generan al girar una figura plana alrededor de un eje. Los principales son el cilindro, el cono y la esfera.

- El cilindro se genera a partir del giro de un paralelogramo alrededor de uno de sus lados, generalmente un rectángulo o un romboide.

- El cono se genera a partir del giro de un triángulo rectángulo a partir de uno de sus catetos.

- La esfera se genera a partir de un semicírculo alrededor de su diámetro.

Cada uno de ellos tiene una serie de fórmulas y algoritmos para calcular su área y su volumen. Al ser cuerpos de revolución, todos ellos dependen completamente del número π.

¿Y cómo podemos representar los cuerpos geométricos y las figuras planas? Pues a través de los llamados sistemas de representación, que definió el teórico Monge, añadiendo a las Matemáticas el término de Geometría Descriptiva.

Los modelos 2D y 3D son muy variados, pero principalmente tenemos algunos que reconoceréis, como el dibujo, el croquis, la fotografía o el propio plano en sí.

Es por esto que la intervención educativa en geometría no puede ser solo conceptual, sino también basada en la realidad y representativa, y sobre todo práctica, ya que la geometría es uno de los ámbitos de las Matemáticas que más difícil resulta para el alumnado de Educación Primaria.

El Decreto 81/2022 incluye los saberes básicos relacionados con la geometría y la percepción espacial con el Bloque C: Sentido Espacial. El trabajo de la geometría contribuye al desarrollo de 5 de las 8 competencias clave del currículo: La Competencia en Comunicación Lingüística (CCL), la Competencia Matemática y Competencia en Ciencia, Tecnología e Ingeniería (STEAM/STEM), la Competencia Digital (CD), la Competencia Personal, Social y de Aprender a Aprender (CPSAA), y la Competencia Emprendedora (CE).

Existen múltiples recursos, tanto físicos como digitales, que permiten trabajar la geometría en el aula, como por ejemplo el Tangram o el Geoplano, pero sin duda el mejor de todos es el programa Geogebra. Tiene casi todas las funciones que se puedan necesitar en Matemáticas, desde una hoja de cálculo, un eje de coordenadas, incluso funciones en 3D para representar cuerpos geométricos. Además, como bien sabemos, los recursos TIC vienen muy bien de cara a mejorar el aprendizaje significativo de los saberes básicos del currículo.

¿Qué os parece? Este sí que ha sido un tema DENSO. Pero ya solo quedan 4... Cuenta atrás en marcha. ¡Nos vemos!

Read More

Tema 23: Las magnitudes y su medida en Educación Primaria

¡Bienvenidos una vez más! Seguimos nuestra andadura en el camino del opositor, pero ya nos queda muy poco para terminar con el temario. Hoy vamos a ver el tema 23, correspondiente a las magnitudes y su medida en Educación Primaria.

La Oficina Internacional de Pesos y Medidas, dependiente del Sistema Internacional, define magnitud como el atributo de un fenómeno, cuerpo o sustancia que puede ser distinguido cualitativamente y determinado cuantitativamente.

Hay dos tipos de magnitudes: Escalares, medidas por un número + la unidad, y Vectoriales, que están medidas por un vector, que es un segmento orientado con módulo, dirección y sentido.

Existen 7 principales magnitudes que el Sistema Internacional define como las principales, que son las de la tabla de arriba. Sus definiciones son realmente complejas.

A partir de las magnitudes fundamentales del Sistema Internacional, se derivan una gran cantidad de magnitudes que utilizan una o más de las magnitudes fundamentales para poder medirse. Son las magnitudes derivadas, y algunas de ellas las podemos ver en la tabla de arriba.

De las que hemos visto, las más conocidas serían las de la fuerza, el potencial eléctrico o la temperatura, que aparte de medirse en Kelvin, se mide también en grados Celsius o centígrados, o en grados Fahrenheit.

Todas y cada una de las magnitudes tienen múltiplos y submúltiplos, que permiten ordenarlas más fácilmente. Se mantiene el símbolo de la unidad de medida, pero en función de si es un múltiplo o un submúltiplo, se deberá utilizar la unidad seguida de ceros con exponente positivo o negativo. Por todo esto, aparece una clasificación que se deberá tener en cuenta a la hora de escribir las unidades de medida:

A partir de esta tabla podemos deducir que las magnitudes por encima del prefijo tera- se encuentran muy relacionadas con la astronomía y el universo, mientras que las que se encuentran por debajo del prefijo pico- pertenecerían al orden atómico.

Para poder realizar conversiones de unidades a sus respectivos prefijos y sufijos tenemos dos algoritmos: o los factores de conversión, que son algo más complicados de aprender, y la tabla de conversión, que es increíblemente sencilla y que os puedo dejar que veáis aquí.

Las unidades de medida se pueden escribir en forma compleja (con varias unidades a la vez, como por ejemplo 4km 8m), y en forma incompleja (con una sola unidad, por ejemplo 4008m). A la hora de representarlas en forma incompleja, se suele elegir la unidad más pequeña para que quede una cantidad natural.

IMPORTANTE: Una unidad de medida, especialmente el tiempo, NO SE PUEDE ENCONTRAR DE FORMA NEGATIVA. Esto quiere decir que no podemos tener algo que pese -40kg, o la hora de algo sean las -2h.

Antes os he dicho que las magnitudes fundamentales tenían unas definiciones muy complejas... pero ya sabéis que aquí no nos dejamos nada, así que vamos una por una a definirlas (preparaos):

Longitud: Es la distancia entre dos puntos dados. La longitud entre un punto y el mismo es 0, pero la longitud entre dos puntos distintos deberá ser medida a partir de la comparación con una distancia determinada y fija. Esta medida, según el SI es el metro, que se definió como la longitud de la trayectoria recorrida por la luz en un lapso de tiempo de 1/299.792.458 segundos.

Tiempo: Es la magnitud física con la que medimos la duración o separación de acontecimientos sujetos a cambio, permite ordenar los sucesos en secuencias, estableciendo un pasado, un presente y un futuro, y da lugar al principio de causalidad, uno de los axiomas del método científico. Su unidad de medida, el segundo, se define actualmente como la duración de 9.192.631.770 períodos de la radiación correspondiente a la transición entre los dos niveles hiperfinos del estado base del átomo de cesio-133. 

Masa: Se define al fijar el valor numérico de la constante de Planck, h, en 6.626 × 10⁻³⁴, cuando se expresa en la unidad J.s, igual a kg·m²·s⁻¹, según las definiciones del metro y el segundo dadas anteriormente.

Temperatura: Mide el nivel térmico de los cuerpos, es decir su nivel de calor o frío. La unidad de medida es el Kelvin (K), de modo que el 0K es el considerado cero absoluto, ya que, según el científico Lord Kelvin, ningún cuerpo experimenta ningún tipo de enfriamiento por debajo de esa temperatura, y, de la misma manera, sus partículas no pueden alcanzar ninguna clase de movimiento o vibración.

Intensidad de corriente: Es el número de electrones que fluyen por un punto concreto de un circuito eléctrico en un determinado tiempo. La unidad de medida del S.I. es el amperio, que se define como la intensidad de una corriente constante que, mantenida en dos conductores paralelos rectilíneos, de longitud indefinida de sección circular despreciable, colocados a un metro de distancia entre sí en el vacío, produciría entre los conductores una fuerza igual a 2 x 10-7 N/m.

Intensidad luminosa: Se define como la intensidad de la luz en una cierta dirección. La candela, su unidad de medida, es extraída y definida a partir de una fuente lumínica que emite una radiación monocromática de frecuencia 540 x 1012 Hz y cuya intensidad energética en esa dirección es de 1/683 vatios por estereorradián.

Cantidad de sustancia: Es una magnitud que se utiliza esencialmente en procesos químicos. La unidad de medida se denomina mol, y es entendida como el número de entidades elementales equivalente a los átomos existentes en 12 gramos de carbono-12. Actualmente se sabe que ese número de átomos es N= 6,023 x 10^23, llamado constante de Avogadro.

Después de habernos quedado igual con las definiciones del Sistema Internacional de las principales unidades de medida (la verdad es que son complicadas eh, no lo niego), vamos a otro punto vital a la hora de operar con cualquier unidad de medida, que son las estimaciones y aproximaciones.

Estimar es aproximar sin ayuda de instrumentos, es decir, con pura intuición. Aproximar es dar una cantidad cerca de la exacta con ayuda de instrumentos, fórmulas... Así, encontramos dos formas de representar el error: absoluta (valor real - aproximado), y relativa (que se define con la fórmula Er = (Ea/Valor real) x 100.

La forma más conocida y científica de redondear es a través de la notación científica. Ésta consiste en colocar un número muy grande o muy pequeño con una parte decimal, una parte entera y la unidad seguida de ceros en función de la cantidad de cifras que se desee aproximar. Por ejemplo, la notación científica sería algo parecido a lo que hemos visto en la definición de masa: 6.626 × 10⁻³⁴

El Decreto 81/2022 incluye un sentido exclusivamente para entender todo lo relacionado con las unidades de medida, llamado el Sentido de la Medida. El hecho de trabajar con esto permite al alumnado desarrollar hasta 5 de las 8 competencias clave del currículo: la Competencia en Comunicación Lingüística (CCL), la Competencia Matemática y Competencia en Ciencia, Tecnología e Ingeniería (STEM), la Competencia Digital (CD), la Competencia Personal, Social y de Aprender a Aprender (CPSAA) y la Competencia Emprendedora (CE).

Los recursos didácticos a utilizar en las Unidades Didácticas sobre las unidades de medida son casi ilimitados. Tanto que nos sirven monedas, reglas, relojes... Normalmente la intervención educativa en Educación Primaria no muestra muchas de las unidades de medida descritas anteriormente. De hecho, en Primaria entran las medidas básicas de longitud, masa, capacidad, superficie, volumen, amplitud angular, tiempo y dinero.

¿Qué os parece? Ya solo quedan 2 temas de Matemáticas... ¡Ya estamos terminando! ¡Nos vemos!

Read More

Tema 22: El aprendizaje de los números y el cálculo numérico en Educación Primaria

¡Bienvenidos una vez más! Hoy vamos a ver uno de mis temas favoritos, ya que como es íntegramente de números y Matemáticas... Vamos a ver qué importancia tienen los números en Educación Primaria.

El concepto de número es uno de los más abstractos que existen. Se dicen que subyacen a todo el proceso de medición, ordenación, operación... Y el cálculo numérico, por tanto, es aquel que se sirve de las operaciones y procedimientos con los números para ejecutar acciones Matemáticas.

Pero si lo pensamos bien... el concepto de número engloba a cantidades tan importantes, como el 0, el 1, el número π, el número e... Y hay muchísimos más. Existen números naturales, enteros, complejos, reales, amigos, primos, gemelos... Pasamos a detallarlos con algunas de sus propiedades.

 

ℕ: Es el conjunto de los números naturales. Son aquellos que, fundamentalmente, sirven para contar. Se dividen en dos: N y N_0. La diferencia entre ellos es que N_0 incluye al número 0 dentro de los naturales, mientras que N lo excluye. El conjunto de los números naturales es infinito.

Como bien sabemos, hay 6 operaciones básicas para realizar con los números naturales: La suma, la resta, la multiplicación, la división, la potencia y la raíz cuadrada. De ellas, la suma y la multiplicación son las más elementales.

A continuación os dejaré unas infografías que, por orden, explicarán las propiedades de la suma y la multiplicación:

Pero para las propiedades de las potencias hay algo más que esto, ya que funcionan de manera algo diferente a la multiplicación:

Por orden, de izquierda a derecha, os las explico:

1) Todo potencia de base 1 elevada a N siempre es 1.

2) Todo número elevado a 1 es sí mismo.

3) Todo número A elevado a 0, con A distinto de 0, es 1. (Esto no es cierto si tenemos en cuenta que el límite de A cuando A tiende a 0 es 1 por la propia regla. Ahora, 0 elevado a 0 es otro cantar si hablamos de indeterminación en vez de resultado 1)

4) En una multiplicación de potencias de la misma base, se deja la base y se suman los exponentes.

5) En una división de potencias de la misma base, se deja la base y se restan los exponentes.

6) Cuando una potencia se eleva a otra potencia, se deja la base y se multiplican los exponentes.

7) Cuando una fracción se eleva a una potencia, se deja la base y se elevan tanto el numerador como el denominador al exponente.

8) Cuando un número A se eleva a -1, su resultado es su inverso en forma de fracción, con A distinto de 0 (aunque se puede entender que si A tiende a 0, el resultado es + ∞)

9) Cuando una fracción se eleva a -1, su resultado es la fracción inversa de la primera.

10) Cuando un número A se eleva a un exponente negativo distinto de 1, su resultado es la fracción inversa con denominador en forma de la potencia elevada a exponente positivo, siendo A distinto de cero. (En este caso, volveríamos al ejemplo del caso 8).

11) Cuando una fracción se eleva a un exponente negativo, su resultado es la inversa con cada factor elevado al exponente.

La resta, la división y la raíz cuadrada no comparten ninguna de estas propiedades, al tener posibles soluciones algebraicas que no sería posible encuadrar en N.

Z: Es el conjunto de los números enteros. En él se incluyen todos los números naturales (o enteros positivos), el 0 y los naturales negativos (o enteros negativos). Es un conjunto infinito y, de hecho, es un conjunto infinito más grande que el de los números naturales N.

Comparten operaciones con los números naturales y sus propiedades, pero por lo general se utiliza el valor absoluto de los números y se calcula con ellos. El valor absoluto es considerado como el número natural que no tiene signo, y que se representa con dos barras verticales en medio: ${\displaystyle |x|}$ 

En la potenciación surge una nueva propiedad, que dice que cualquier entero elevado a un exponente N, debe representarse así:

1) Si un entero positivo o negativo se eleva a un exponente positivo o negativo par, su potencia será positiva.

2) Si un entero positivo o negativo se eleva a un exponente negativo impar, su potencia será negativa.

En este punto entran dos conceptos básicos: Los múltiplos y los divisores y sus acompañantes, el mínimo común múltiplo y el máximo común divisor. Para hallarlos, debemos:

− Dados dos números enteros a y b, se llama MCD de a y b al mayor entero que divide a ambos. Para calcularlo: se tomará el producto de los factores primos comunes con el menor exponente de sus descomposiciones.

− Dados dos números enteros a y b, se llama mcm de a y b, al menor entero que es múltiplo de ambos. Para calcularlo se tomará el producto de todos los factores primos con el mayor exponente de sus descomposiciones.

Aquí entran en juego los llamados números primos, que son todos aquellos que se pueden dividir únicamente entre 1 y entre sí mismos de forma exacta. Unidos a ellos existen los llamados criterios de divisibilidad, y junto a estos, unos números primos llamados de Mersenne, de la forma , para N primo. Como éstos se conocen aproximadamente unos 50. El más alto sería el (M_82.589.933).

 

${\displaystyle \mathbb{Q}}$: Es el conjunto de los llamados números racionales, que son todos aquellos que se pueden expresar en forma de cociente de dos números enteros. En este conjunto se incluyen todos aquellos números conocidos como fracciones, que es la expresión de un cociente de dos números.

Las fracciones también tienen sus propiedades, que serían:

1) La multiplicación de fracciones se realiza multiplicando numeradores y denominadores simultáneamente.

2) La división de fracciones se puede realizar operando el producto cruzado de ambas.

3) La suma (o resta) de fracciones con igual denominador se realiza dejando el mismo denominador y sumando los numeradores.

4) La suma de fracciones con distinto denominador se puede realizar obteniendo el mcm de los denominadores y multiplicando cada numerador por el factor sobrante.

5) Una fracción irreducible es aquella que no se puede dividir más veces por el mismo factor primo. De hecho, la fracción simplificable es aquella que se puede dividir por uno o más factores primos comunes al numerador y al denominador.

6) Cuando dos fracciones son equivalentes, su producto cruzado también lo es.

Al hablar de números racionales también encontramos los números decimales, que serán racionales o irracionales (I) en función de su desarrollo decimal. Por esto, los números decimales exactos, como el 1'25 o el 0'97 son racionales, mientras que π, al tener infinitos decimales no periódicos, se dice que es irracional y trascendente.

El sistema de numeración decimal (o de base 10) no es el único que existe. Hay infinitos más, pero los más conocidos son el binario (que se usa en informática), el octal (base 8) y el hexadecimal (base 16), que se usan también en informática, pero específicamente en criptografía, y el sistema en base 36 o alfanumérico, que es la base de múltiples operaciones y procesos matemáticos superiores.

En Educación Primaria nos interesan otros dos que pasan algo más desapercibidos, como son el sistema sexagesimal (base 60), que tiene como su origen la división del círculo en 360 partes (2πrad), o el sistema de numeración romana (I, V, X, L, C, D y M), que actualmente se utiliza para nombrar siglos de la historia, entre otros usos.

La relación entre los infinitos números queda demostrada en esta pequeña infografía. Cada conjunto es más grande que el anterior, de ahí que haya infinitos más grandes que otros. En Educación Primaria nos detendremos en R, mientras que en Educación Secundaria y Bachillerato introduciremos la idea de C, o los números complejos.

El Decreto 81/2022, aunque no contempla los números enteros como parte de los saberes básicos del currículo, englobaría todos estos conceptos matemáticos dentro del Sentido Numérico. Además, estos contenidos básicos para los alumnos y alumnas de Primaria, favorecen al desarrollo de las competencias clave del currículo, en especial la Competencia Matemática y Competencia en Ciencia, Tecnología e Ingeniería o STEAM/STEM.

¡WOW! Menudo tema nos ha quedado... ¿Qué os parece? Si os digo la verdad, he disfrutado muchísimo escribiendo esto para todos vosotros... La pena es que ya solo quedan 6 temas para acabar con esto... Que no son pocos eh... Pero ya va quedando menos. ¡Nos vemos!

Read More

Tema 21: La resolución de problemas en la Educación Primaria

¡Bienvenidos de nuevo! Ya va quedando muy poco para terminar nuestra parte de temas del camino del opositor. Hoy vamos a ver el tema 21, correspondiente al proceso de resolución de problemas en Matemáticas.

Según Polya, uno de los mayores creadores del algoritmo básico de resolución de problemas en Educación Primaria, un problema matemático es aquel que necesita de una situación que necesita ser resuelta y para la que el individuo no tiene un camino rápido para llegar hasta su solución.

Normalmente un problema, para que realmente sea considerado como ello, debe presentar tres requisitos:

1) Aceptación. El individuo o grupo, debe aceptar el problema, debe existir un compromiso formal, que puede ser debido a motivaciones tanto externas como internas. 

2) Bloqueo. Los intentos iniciales no dan fruto, las técnicas habituales de abordar el problema no funcionan. 

3) Exploración. El compromiso personal o del grupo fuerza la exploración de nuevos métodos para atacar el problema.

El currículo de la Educación Primaria, determinado por el Decreto 81/2022, indica que la resolución de problemas es uno de los métodos más eficaces para aprender Matemáticas. Además, la resolución de problemas favorece al desarrollo de 4 de las 8 competencias clave: CCL (Competencia en Comunicación Lingüística), STEAM/STEM (Competencia Matemática y Competencia en Ciencia, Tecnología e Ingeniería), CPSAA (Competencia Personal, Social y de Aprender a Aprender), y CE (Competencia Emprendedora).

Por otra parte, la resolución de problemas, al ser una de las actividades más complejas que se les puede asignar a un alumno, es incluida como saber básico dentro de los 6 sentidos que propone el Decreto 81/2022. Los problemas tienen múltiples clasificaciones, así que vamos a ir analizándolos poco a poco:

Problemas aritméticos: Son aquellos que en su enunciado presentan datos en forma de cantidades y necesitan de la realización de operaciones aritméticas para su resolución. Entre ellos hay dos subdivisiones:

Problemas de adición - sustracción, entre los que se engloban problemas de cambio, problemas de combinación, problemas de comparación o problemas de igualación. En todos ellos, se han de utilizar operaciones aritméticas de suma y resta.

Problemas de multiplicación - división, entre los que se incluyen problemas de reparto, problemas de factor N (donde una cantidad se multiplica o divide N veces), problemas de razón y problemas de producto cartesiano (que no tiene relación con las coordenadas cartesianas).

Problemas geométricos: Son aquellos en los que se encuentran incógnitas de carácter geométrico, con diferentes formas y elementos y en figuras generalmente de 2 y 3 dimensiones. Hasta el Bachillerato no se incluiría una cuarta dimensión, que tendría como acompañante a los números complejos en la resolución de los problemas.

Problemas de lógica: Son los que permiten desarrollar destrezas que permiten afrontar situaciones de componente lógico. Entre estos problemas se encontrarían los problemas de curiosidad matemática.

Problemas de recuento sistemático: Son problemas que tienen más de una solución. Por lo general, la solución debe ser algebraica. Encontraríamos aquí todos aquellos problemas relacionados con las ecuaciones, el álgebra, las derivadas y las integrales (aunque estos últimos prácticamente sirven para formular teoremas y axiomas matemáticos).

Problemas de razonamiento inductivo: Enuncian propiedades numéricas o geométricas a partir del descubrimiento de regularidades. Existen tantos como teoremas, axiomas, conjeturas... matemáticas haya. Los más famosos serían la Hipótesis de Riemann o la Conjetura de Fermat.

En este vídeo tenemos algunos ejemplos de problemas aritméticos que serían perfectamente utilizables tanto en Primaria como en Secundaria. Es en éstos donde nos vamos a centrar, ya que debemos explicar el método de Polya de 1987, quien crea una estrategia básica de resolución de problemas en cuatro fases:

Comprensión del problema: Implica entender tanto el texto como la situación que nos presenta el problema y comprender qué debe hacerse con la información que nos es aportada.

Elaboración de la estrategia: Es la parte fundamental del proceso de resolución de problemas. Una vez comprendida la situación planteada y teniendo clara cuál es la meta a la que se quiere llegar, es el momento de planificar las acciones que llevarán a ella.

Aplicación de la estrategia: Consiste en la puesta en práctica de cada uno de los pasos diseñados en la planificación. Se debe comprobar si los pasos dados son correctos.

Visión retrospectiva: Un problema no se termina cuando se ha hallado la solución. Se debe realizar la revisión del proceso seguido para analizar si es o no correcto el modo como se ha llevado a cabo.

Para continuar con la resolución de un problema, debemos entender el concepto de heurística. Éste se entiende como el conjunto de estrategias y razonamientos mentales que se realizan a la hora de resolver un problema. Son heurísticos todos aquellos planteamientos que circulan en la mente a la hora de entender una situación problemática.

Las técnicas heurísticas son enormemente valiosas para el profesor, que debe ser capaz de controlarlas y transmitirlas a los alumnos para que comprendan el proceso de resolución de problemas. Además, este proceso está ligado a una planificación de los recursos necesarios para su solución, es decir, se deben optimizar los recursos, tanto matemáticos como mentales, que se emplean para la resolución de un problema.

¿Qué os parece? Seguimos avanzando en los temas de Matemáticas... y el que viene es casi mi favorito. ¡Nos vemos!

Read More

Tema 20: El área de Matemáticas en la Educación Primaria

¡Bienvenidos una vez más! Continuamos con nuestro camino del opositor, pero esta vez estoy más contento, porque por fin llegamos a la asignatura de Matemáticas, la que ha sido siempre mi preferida y la que sería mi principal asignatura a impartir si llego a un cole. Atentos.

¡Qué decir de las Matemáticas! Son definidas como un conjunto de saberes asociados en una primera aproximación a los números y a las formas que se van progresivamente completando hasta constituir un modo valioso de analizar situaciones variadas.

Su enfoque se divide en cuatro vertientes, al igual que las asignaturas de Lengua y Conocimiento del Medio. Sus perspectivas psicológica, pedagógica, epistemológica y sociológica permiten entender a las Matemáticas como una materia con carácter globalizador.

Las Matemáticas fundamentalmente contribuyen a impulsar procedimientos y actitudes asociadas con el autoconcepto y la autoestima, estimula capacidades como la forja de un pensamiento matemático, y sobre todo, se encarnan en un sentido eminentemente experiencial, con lo que las Matemáticas se basan fundamentalmente en prácticas y más prácticas, así como en aplicaciones a la vida cotidiana.

Toda actuación docente se debe basar en dos puntos:

Primero, en los principios de intervención educativa, que permiten que exista una coherencia horizontal (entre áreas) y vertical (entre cursos), así como ayudan a crear un sustento metodológico sobre el que trabajar en el aula y crear un modelo de acción educativa eficaz.

Segundo, en el desarrollo combinado de estrategias didácticas de exposición e indagación que permitan que el alumno se motiva y crezca su interés por aprender.

El tratamiento del currículo es bastante complejo en lo relativo a las dimensiones educativas que las Matemáticas suponen para el desarrollo integral del alumnado. Pasamos a ver los aspectos fundamentales que resaltan la Ley Orgánica 3/2020 (LOMLOE), y su desarrollo curricular, en el Real Decreto 157/2022 y el Decreto 81/2022:

Las Matemáticas tienen como base fundamental la Competencia Matemática y Competencia en Ciencia, Tecnología e Ingeniería (STEM/STEAM). Aunque en el área se debe trabajar todas las competencias por su carácter interdisciplinar, el área de Matemáticas también contribuye en buena medida al desarrollo de la Competencia Digital (CD).

Por otra parte, el área posee un objetivo de etapa específico para ella, el G, que dice: Desarrollar las competencias matemáticas básicas e iniciarse en la resolución de problemas que requieran la realización de operaciones elementales de cálculo, conocimientos geométricos y estimaciones, así como ser capaces de aplicarlos a las situaciones de su vida cotidiana.

Los saberes básicos de este área son ligeramente diferentes a los de otras áreas, ya que en vez de agruparse en bloques como tal, se agrupan por sentidos. Así pues, el desarrollo curricular diferencia hasta 6 sentidos claramente diferenciados. Los describimos:

 

Sentido numérico: se caracteriza por el desarrollo de destrezas y modos de pensar basados en la comprensión, la representación y el uso flexible de números y operaciones para, por ejemplo, orientar la toma de decisiones.

Sentido de la medida: se caracteriza por la comprensión y comparación de atributos de los objetos del mundo natural. Entender y elegir las unidades adecuadas para estimar, medir y comparar; utilizar instrumentos adecuados para realizar mediciones, y comprender las relaciones entre magnitudes, utilizando la experimentación, son sus elementos centrales.

Sentido espacial: es fundamental para comprender y apreciar los aspectos geométricos del mundo. Está constituido por la identificación, representación y clasificación de formas, el descubrimiento de sus propiedades y relaciones, la descripción de sus movimientos y el razonamiento con ellas.

Sentido algebraico: proporciona el lenguaje en el que se comunican las matemáticas. Engloba los saberes relacionados con el reconocimiento de patrones y las relaciones entre variables, la expresión de regularidades o la modelización de situaciones con expresiones simbólicas. Dentro de este sentido también se encuentra el pensamiento computacional.

Sentido estocástico: se orienta hacia el razonamiento y la interpretación de datos y la valoración crítica, así como la toma de decisiones a partir de información estadística. También comprende los saberes vinculados con la comprensión y la comunicación de fenómenos aleatorios en situaciones de la vida cotidiana.

Sentido socioafectivo: integra conocimientos, destrezas y actitudes esenciales para entender las emociones. Manejarlas correctamente mejora el rendimiento del alumnado en matemáticas, combate actitudes negativas hacia ellas, contribuye a erradicar ideas preconcebidas relacionadas con el género o el mito del talento innato indispensable y promueve el aprendizaje activo.

Las Matemáticas están EN TODAS PARTES. Por esto, la relación que tiene con otras áreas del currículo, como puede ser el Conocimiento del Medio, es tan significativa. Si nos ponemos a pensar, estamos rodeados completamente de conceptos matemáticos.

¿Qué os parece? Algún día si apruebo la oposición abriré una etiqueta con curiosidades matemáticas, que conozco bastantes. ¡Seguimos avanzando, ya queda menos!

Read More